20.05.2002 - 27.05.2002

Vorläufige Version der Dokumentation

Projekt: Multi

 

Mein Multi Projekt heißt so, weil es folgende grafische Bereiche beinhaltet: Parabeln, Fraktale und Landschaften.

Zu den Parabeln:

- Die Variable Normalparabel x²:

Hier werden etwas umständlich, weil diese Routine schon früher von mir geschrieben wurde, Werte eingelesen. Der X-Wert wird immer um 0,01 erhöht, um mehr Pixel und damit deutlichere Grafiken zu

bekommen, und der Y-Wert mit y = x² gezeichnet und die restlichen Werte b und c von bx + c hinzuaddiert.

- Die Variable Normalparabel x² zum Berechnen:

Bei der Berechnung werden die Werte eingelesen und 1. Als Formel ausgegeben. 2. Der berechnete Scheitel b und c von bx + c ausgegeben. 3. Die Steigung a von ax² ausgegeben.

- Die Variable Parabel x³:

Hier wurde die Routine von der Normalparabel genommen und vereinfacht und die Werte eingelesen.

Wobei bei den Werten av und bv als Variabel eingelesen werden um nicht nur Integer-Werte einlesen zu können die natürlich, also nicht z.B. 0.5 sein können. Dann wird der X-Wert wird immer um 0,01 erhöht, um mehr Pixel und damit deutlichere Grafiken zu bekommen, und der Y-Wert mit y = ax³ + bx² gezeichnet und den restlichen Wert c hinzuaddiert.

- Die Variable Wurzelfunktion:

Die Wurzelfunktion wurde durch die Umänderung von der x³-Parabelfunktion gewonnen. Der Y-Wert wurde mit Quadratwurzel von ax gezeichnet.

Zu dem Bäumchen:

Hier wurde ein Basic Programm in Pascal / Delphi umgeschrieben. Leider wird kein Bäumchen dargestellt.

Zu den Fraktalen:

-Mandelbrot Fraktal 2D:

Bei dem Fraktal werden viele Werte eingelesen, wie z.B.: Zoom, Streckung, Farbart, Farbtiefe und Farbunterschiede. Diese werden dann in eine, sich ständig mit veränderten Faktor, wiederholende Formel eingefügt. Diese erzeugt dann für jedes Pixel eine andere Farbe.

-Mandelbrot Fraktal 2D schräg:

Hier wird dasselbe wie im normalen Mandelbrot gemacht, mit dem Unterschied, dass beim Zeichen noch ein Faktor hinzukommt, die mit dem Y-Wert wächst und so die Schräge macht.

-Mandelbrot Fraktal 3D:

Bei dem 3D Fraktal wurde die Art der Farbe eingelesen, und durch einen Faktor ersetzt, der zum Y-Wert hinzuaddiert wird. So erhält man unterschiedlich hohe Ebenen, die, wenn man sie schräg stellt 3D aussehen.

Zu den Landschaften:

-Landschaft mit Parabelfunktion:

Bei der Parabellandschaft wurde eine Parabel hintereinander mit verschieden a Werten von ax² gezeichnet, dadurch erhält man eine Parabelschar, die wie ein Trompetentrichter aussieht. Man kann auch andere Werte für a eingeben, für die dann der Trichter flacher (z.B.: 0.05) oder steiler (z.B.: 5) wird.

 

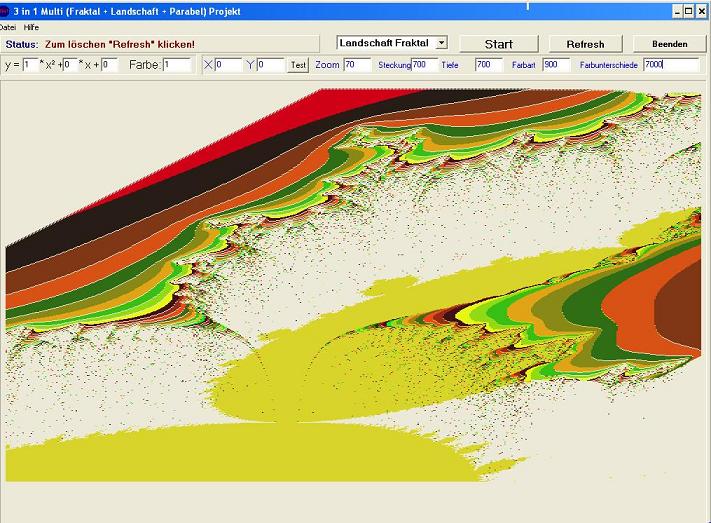
-Landschaft mit Fraktalfunktion:

Hier wurde eine normale Landschaft genommen und statt der verschieden Routinen für die Variabel a wurde eine normale Fraktalformel eingesetzt. Dies war eine schwierige Aufgabe da man trotzdem variabel Werte für die Fraktalformel eingeben können musste.

-Landschaft mit Fraktalfunktion in einem neuen Fenster:

Bei dieser Landschaft in einem neuen Fenster, das bei der Bildschirmauflösung von 1024x 768 Pixeln, die Startleiste und die Titelzeile des Fensters nicht mehr zeigt, werden keine extra Werte eingelesen, sondern nur die Standartwerte benutzt. Die Farben werden teilweise durch Zufall, zudem festgelegte Werte hinzumultipliziert und hinzuaddiert werden, bestimmt. Dem Programm wurden bestimmte Höhenabschnitte vorgegeben, bei denen es eine bestimmte Farbe zeichnen musste. Dies ergibt insgesamt eine sehr schöne Herbstlandschaft mit einem unglaublich blauen See der die Form eines Mandelbrotfraktales hat.

-Landschaft mit Punkten:

Hier wird eine beliebige Zahl aus dem Zahlenraum von 0 bis 500 herausgesucht, durch 10 geteilt und gerundet. Dann wird diese, jedes Mal andere Zahl i bestimmten Abständen als dicker Punkt gezeichnet. Je nach Höhe wird der Punkt in einer bestimmten Farbe gezeichnet.

-Landschaft mit Stäbchen (Insel):

Bei der Landschaft aus Stäbchen werden die einzelnen Punkte als Linien von der 0 Linie zu dem Punkt gezeichnet. Wenn man keine Abstände zwischen den einzelnen Linien wählt, ergibt das dieses Bild.

-Landschaft Horizontal:

Hier wurden die einzelnen Punkte mit Linien verbunden, wichtig war, dass am jeweiligen Ende der X-Achse keine Linie zu nächsten Punkt auf der nächsten Y-Achse gezeichnet werden durften. Eine ziemlich komplizierte Formel rechnet mithilfe des X Wertes, dessen Sinus und Zufallswerten, eine Höhe aus, für die je nach Höhe verschiedene Farben verwendet werden.

-Landschaft Horizontal mit variablen Farbwerten:

Hier wird dasselbe wie oben gemacht, mit dem Unterschied, dass man die Farben selber auswählen kann, damit ergeben sich dann fließende Überläufe.

-Landschaft Vertikal:

Hier wird die Horizontale Landschaft einfach vertikal gezeichnet. Das Ergebnis ähnelt einer Weinbergslandschaft.

Zu dem Gitternetz:

Bei dem Gitternetz werden dunkelgraue Striche mit 10 Pixeln Abstand auf der X in Y Achsenebeneinadergelegt.

Zu der Skala:

Hier werden 2 schwarze Striche gezeichnet, die auf dem Gitternetz liegen. Dann wird der X und der Y Wert in 50ger Schritten hochgezählt und immer die durch 50 geteilte Zahl abzüglich 500 geschrieben um kleinere Einheiten zu bekommen und um Minuswerte zu bekommen.

 

Zu der Grafischen Aufteilung:

Eingabefläche für Parabeln: Dieser Teil erscheint farbig (blau) wenn er benutzt wird. Hier gibt man den a- Wert, die Farbe und die vertikale und horizontale Verschiebung an. Bei der x³ Parabel werden die Werte geringfügig verändert damit man das a von x³ und x² und die horizontale Verschiebung ändern kann. Bei der Wurzelfunktion wird anstatt y=[ ]*x²+[ ]x+[ ] die Maske y=[ ]-´x` [ ]*x+[ ] verwendet. Das -´x` soll Wurzel aus x bedeuten.

Eingabefläche für Fraktale: Dieser Teil erscheint farbig (blau) wenn er vom Programm eingelesen wird. Man kann hier die X und Y Verschiebung bestimmen, und wenn man den Button Test anklickt, erscheint ein Fadenkreuz. Man kann auch noch die Streckung, den Zoom, Farbtiefe, Farbart, Farbunterschiede und je nach Fraktal den 3D-Wert bestimmen.

Statusleiste: Hier stehen immer Informationen zu dem jeweiligen ausgewählten Objekt. Beim Beginn des Programms wird hier noch die Zeit angezeigt.

Auswahlmenü mit Start-, Refresh- und Beenden Button: Mit dem Auswahlmenü wählt man das gewünschte Objekt aus. Beim Klick auf den Startbutton beginnt das Programm zu zeichnen. Nach Beendigung des Zeichnens klickt man auf den Refreshbutton, dann wird ein graues Rechteck über die ganze Zeichenfläche gemalt und man erhält den Ausgangsbildschirm. Wenn man nicht mehr mit dem Programm arbeiten will, klickt man auf den Beendenbutton, worauf sich eine Messagebox öffnet, und überprüft, ob man wirklich aufhören will.

Menü mit Datei (Ende) und Hilfe (Über..., Info): Über Datei-Ende passiert dasselbe wie wenn man auf den Beendenbutton klickt. Wenn man auf Hilfe-Über... oder auf Hilfe-Info öffnet man ein neues Fenster, indem man entweder die Dokumentation auswählen kann oder Informationen über den Programmierer.

Zu den programmiertechnischen Details:

var Present: TDateTime; Year, Month, Day, Hour, Min, Sec, MSec: Word; begin Present:= Now; DecodeDate(Present, Year, Month, Day); DecodeTime(Present, Hour, Min, Sec, MSec);	Zum Auslesen der Zeit. Werte sind in: Year, Month, Day, Hour, Min, Sec, MSec
Application.MessageBox(´text´,´Titel´,Button)	Eine Messagebox erstellen. Man kann als Button z.B.: OK oder Ja / Nein.
with Paintbox1 do begin Canvas.Pen.Color := clbtnface; {Refresh} Canvas.Pen.Width := 0; canvas.brush.color:= clsilver; canvas.rectangle(0,0,1400,700);	Eine Routine, bei der 1. die Paintbox initialisiert wird. 2. die Farbe des Stiftes. 3. Die Farbe mit der das Rechteck angemalt wird und 4. Das Rechteck mit den Eckpunkten 0,0 und 1400,700
Canvas.Pen.Width := 1; canvas.MoveTo(500,0); canvas.LineTo(500,1400);	Eine einfache Linie von 500,0 nach 500,1400 mit der Breite 1.
f:=strtoint(edit4.text);	Das Einlesen eines Wertes aus Edit4 in die Integer Variable f.
canvas.pixels[x, y]:=f;	Ein Pixel mit den Koordinaten x und y und der Farbe f
canvas.Font.Color:= 1; canvas.font.Size:= 10; canvas.TextOut(10,1,TEXT);	Das Einfügen eines Textes mit der Farbe 1, der Größe 10 und den Koordinaten 10,1 in eine Paintbox.
a:=random(50); canvas.Pen.color := clgreen; if a < 10 then canvas.Pen.color := clblue; if a < 0 then canvas.pen.color := clblack; if a > 40 then canvas.Pen.color := clgray;		So werden die verschiedenen Farben das Pixel zugeordnet.Wenn der Wert a kleiner als 10 ist, wird ist blau, er kleiner als 0, wird das Pixel schwarz und ist er größer als 40, wird das Pixel grau. Ansonsten wird das Pixel grün, das entspricht dem Bereich zwischen 10 und 40.
a:=round((((x-(y/10))+10)+sin(x))+random(round(x/2)));		Dies ist eine sehr komplizierte Berechnung für den Wert a. Es sieht wie eine, nach dem X-Wert ansteigende Landschaft aus. (Landschaft Horizontal)
if ((y > -1) and ((x > 0) and (x < 610))) then canvas.lineto(x,y); canvas.moveto(x,y); canvas.lineto(x,y); if ((y > -1) and ((x > 0) and (x < 610))) then canvas.moveto(x,y);		So werden die einzelnen Punkte verbunden, und wenn der X-Faktor am Ende ist, wird keine weitere Linie gezeichnet, weil sie sonst quer durch das Bild liefe.
procedure TForm1.ComboBox1Change(Sender: TObject); begin if ComboBox1.text = Gitternetz then begin edit1.Font.Color:=clblack; label2.Font.Color:=clblack; label2.caption:='y ='; edit1.text:='1';		Hier wird, immer wenn sich die Combobox verändert, überprüft, was ausgewählt wurde, und der entsprechende Bereich durch Farbe gekennzeichnet. Hier im Beispiel bleibt edit1 und entsprechend label2 schwarz. Nun wird noch der Inhalt verändert, in dem Beispiel ist das der Standart Wert.
var av:variant; av:=edit1.text;		Die Variable ist als variant deklariert, d.h. sie kann alles sein, auch Zahlen kleiner als 0. Dies wird benötigt, um den a-Wert einer Parabel einzulesen, der auch kleiner als 0 sein muss.

 

© 2002 by Peter Munk

P.S.: Ich entschuldige mich für das schlimme Schriftbild. Falls sie sich weiterhin dafür interressieren, können sie gerne die Quelltexte und die Dokumentation von mir bekommen.Hier geht es zum Download(500 KB).

---